Hysteresis Loop Study
A computational micromagnetic study of hysteresis behavior using Ubermag and OOMMF
Hysteresis Loop Study
This project investigates how the shape and area of magnetic hysteresis loops are influenced by spatial variations in exchange energy within nanoscale magnetic systems. Using Ubermag and OOMMF, we modeled cubic materials under cyclic magnetic fields and explored different energy terms, geometric configurations, and system parameters to analyze magnetic behavior.
Project Team
Supervisor: Dr. Bheemalingam Chittari - Website
Assistant Professor, Department of Physical Sciences, IISER Kolkata
Expertise: Computational Physics, Condensed Matter Physics, Nano Science of Materials
Contributors:
Aniket Mishra (23MS096)
Aditya Chaku (23MS095)
BS-MS Students, IISER Kolkata
Scientific Background
Magnetic hysteresis loops reflect how a material’s magnetization changes in response to an external magnetic field. These loops provide critical insights into material properties like coercivity, remanence, and energy loss. Their shape is influenced by:
- Exchange interactions between magnetic moments
- Anisotropy constants and orientation
- DM interaction (Dzyaloshinskii–Moriya)
- Saturation magnetization
- External field strength and direction
Ubermag, a Python interface to OOMMF, enables high-resolution micromagnetic modeling using scripts and parameterized simulations.
Project Objectives
- Simulate hysteresis loops across different spatial exchange energy distributions
- Explore parameter sensitivity in micromagnetic systems
- Visualize magnetization reversal mechanisms
- Develop computational modeling and data analysis skills
- Present loop characteristics under realistic constraints
Default Simulation Setup
- Geometry: Cube of edge length 100 nm
- Mesh: 5 nm × 5 nm × 5 nm
- Exchange Constant (A): 1e-12 J/m
- Uniaxial Anisotropy: K = 4e5, u = (0, 0, 1)
- DM Constant: D = 1e-3 J/m²
- Saturation Magnetization: Ms = 1e6 A/m
- Magnetic Field: Hmin = –1/μ₀ to Hmax = +1/μ₀ over 21 steps

Figure 1. Cubic magnetic system with a mesh size of 5 nm and total size of 100 nm.
Sample Output
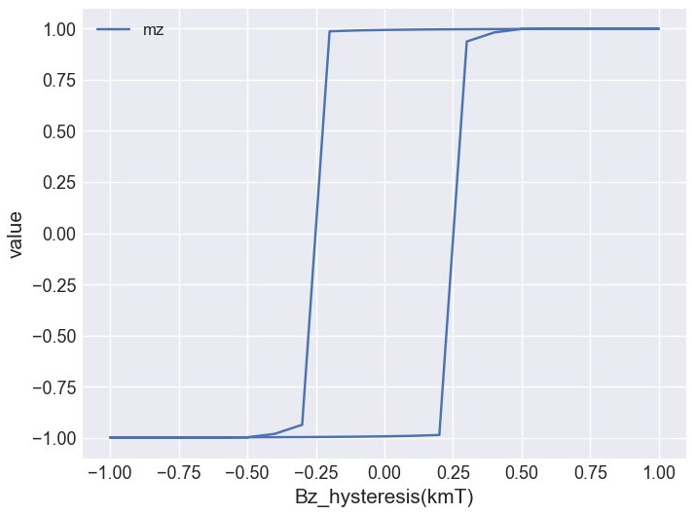
Figure 2. Hysteresis loop from the base configuration showing magnetization vs applied field.
Simulation Variations
1. Geometry and Mesh
- Increasing cube size beyond 80 nm had minimal effect
- Reducing size below 45 nm distorted the loop
- Finer mesh (2 nm) improved resolution; coarser mesh (10 nm) caused loss of detail
2. Energy Parameters
- Exchange Energy: Higher A led to wider loops and sharper transitions
- Anisotropy: Higher K increased coercivity; misaligned u changed loop symmetry
- DM Interaction: High D disrupted loop stability (>2.7e-3 J/m²)
- Saturation Magnetization: Low Ms (<0.3 A/m) caused S-shaped or vanishing loops
3. External Magnetic Field
- Adjusting Hmin and Hmax changed loop span
- Equal but opposite Hmax = –Hmin maintained symmetry
- Directional fields tilted or skewed loop shapes
4. Number of Steps
- More steps gave smoother loops
- Fewer steps produced coarse, stepped plots
- Step size also impacted angular deviation from vertical
Spatial Configurations
- Layered Cubes: Gradual or alternating exchange energy layers
- Pillared Cubes: 5×5 grids of 20 nm pillars with varying A values
- Subdivided Cubes: 3×3×3 inner cubes of 30 nm with descending energy
- Layered Thickness: Variable volume distribution with fixed A, B
- Cube-in-Cube: Core with high A, shell with low A, showing edge–core dynamics
Key Findings
- Spatial distribution of exchange energy alters coercivity and loop structure
- DM interaction can dominate and destroy hysteresis shape at high D
- Magnetic behavior is not solely dependent on size or volume
- External field orientation modifies remanent states
- Loops are highly sensitive to both spatial geometry and field sequence
Conclusion
This study demonstrates how micromagnetic simulations offer insight into complex magnetic interactions in nanoscale systems. By exploring a broad space of energy configurations using Ubermag and OOMMF, the project bridges computational modeling and physical understanding of hysteresis.
Acknowledgments
We thank Dr. Bheemalingam Chittari for his mentorship and deep insight throughout this project. His guidance helped shape both the theoretical framework and computational strategies employed in this work.
This project highlights the use of modern computational tools in micromagnetics to understand fundamental physical phenomena in a highly visual, data-driven way.